BERTScore For LLM Evaluation
Introduction
BERTScore represents a pivotal shift in LLM evaluation, moving beyond traditional heuristic-based metrics like BLEU and ROUGE to a learned approach that captures complex linguistic nuances. Unlike older n-gram-based methods, BERTScore excels at evaluating paraphrasing, coherence, relevance, and polysemy—essential features for modern AI applications.
BERTScore leverages transformer-based contextual embeddings and compares them using cosine similarity to assess the quality of model outputs. Its popularity endures due to its relatively low computational cost and greater interpretability compared to black-box methods like LLM-as-a-judge metrics.
In this article, I’ll explore how BERTScore improves upon traditional evaluation methods, explain its key components, and discuss its role in the broader hierarchy of language model evaluation metrics. Finally, I’ll guide you through implementing BERTScore in Python and show how to integrate it into your evaluation suite using Opik, our open-source framework for LLM evaluation.
The Basics of BERTScore
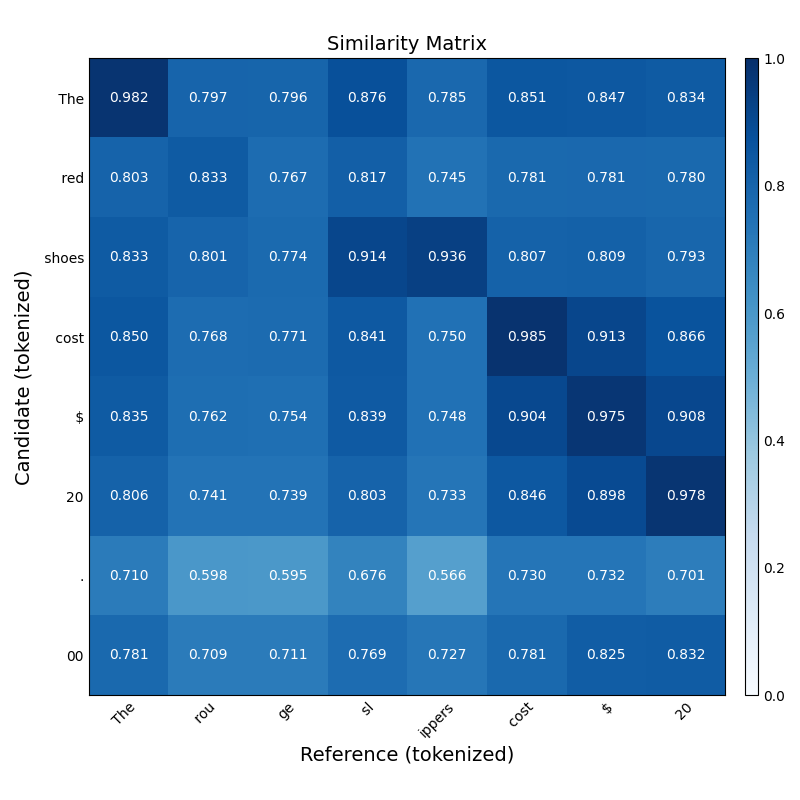
On the surface, BERTScore is, pretty easy to explain: it measures the similarity between tokens in two text sequences by representing them as BERT embeddings and calculating their cosine similarity. For example, given the target sentence, “The red shoes cost $20.00,” BERTScore would rate the candidate sentence “The rouge slippers cost $20” as more similar than “The blue socks cost $20,” even though they have roughly the same number of incorrect tokens.

What makes BERTScore particularly compelling is how it combines different approaches to evaluation. Broadly, LLM evaluation metrics can generally be broken down into three hierarchical categories: heuristic metrics, learned metrics, and LLM-as-a-judge metrics, with BERTScore occupying a unique position within this framework.
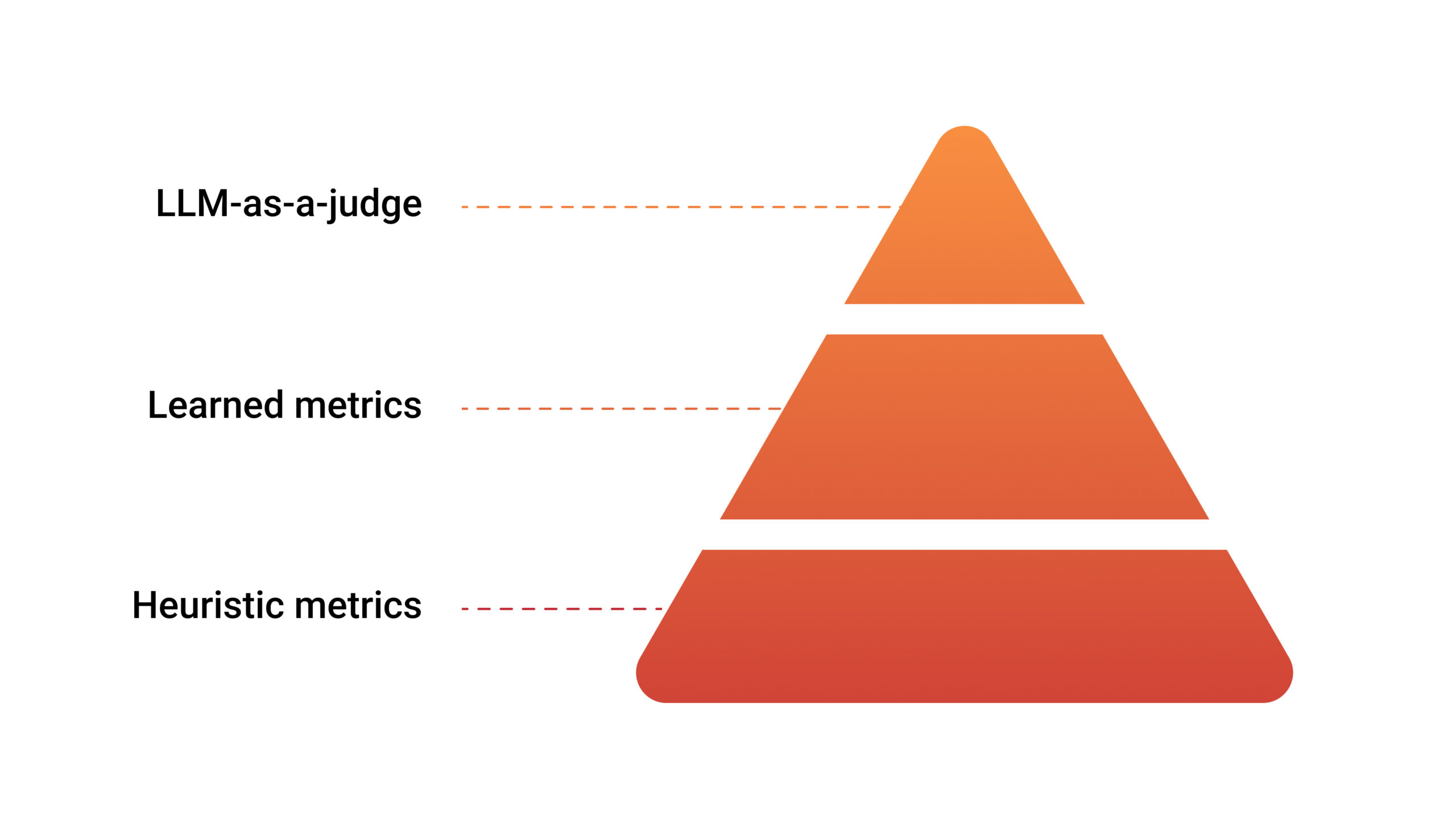
Heuristic Metrics
Heuristic metrics are evaluation measures that are based on predefined, rules-based formulas that quantify specific aspects of model outputs. They are deterministic, interpretable, and computationally efficient. But because they rely on measurable surface-level features like token overlap or exact matches, they often fail to account for the more complex aspects of language, like context, complex semantics, or creativity.
Heuristic metrics include distance metrics, statistical metrics, and overlap or n-gram-based metrics. Popular examples include accuracy, perplexity, BLEU, ROUGE, Levenshtein distance, and cosine similarity.
Learned Metrics
While heuristic metrics rely on fixed, rules-based formulas, learned metrics use machine learning models to score text quality. Typically, these models will represent the evaluated text as some kind of learned embedding.
Because embeddings capture semantic and contextual information, learned metrics provide more depth and nuance than heuristic metrics alone and are effectively able to capture aspects like paraphrasing, coherence, and relevance.
Learned metrics tend to be more aligned with human judgment, but are also more computationally expensive and less interpretable. Examples of learned metrics include BERTScore, BLEURT, COMET, and UniEval.
LLM-as-a-judge Metrics
LLM-as-a-judge metrics are probably the most popular evaluation metrics for evaluating generative language models, and are able to capture the deepest levels of nuance in language. However, they are also the most computationally expensive and present unique interpretability challenges.
LLM-as-a-judge metrics use large language models themselves to act as a “judge” and provide feedback or a quality score based on an evaluation criteria. They are especially useful for open-ended and complex tasks, such as creative writing or reasoning, where predefined metrics may fall short.
BERTScore has the robustness of a learned metric, as it uses BERT’s learned embeddings, but because it is “only” measuring the cosine similarity of token embeddings, it also benefits from the computational efficiency and repeatability of heuristic metrics. If you’re not sure what any of this means, don’t worry, we’ll cover it in the next section!
Theory Behind BERTScore
As we established earlier, BERTScore evaluates the similarity between a reference (ground truth) sentence and a candidate (prediction) sentence by representing their tokens with contextual embeddings and comparing them using cosine similarity. Let’s break that down, starting with a little background.
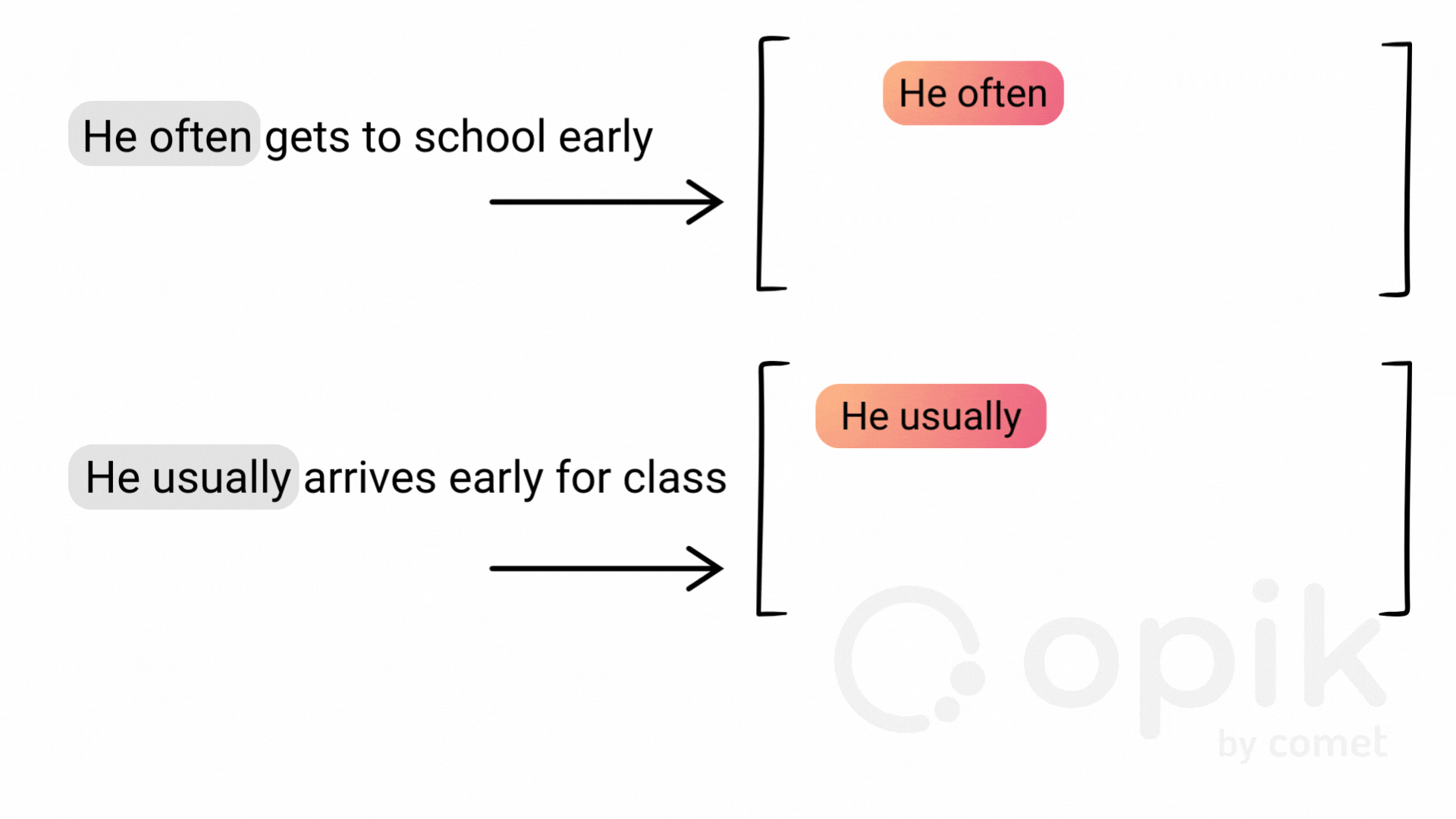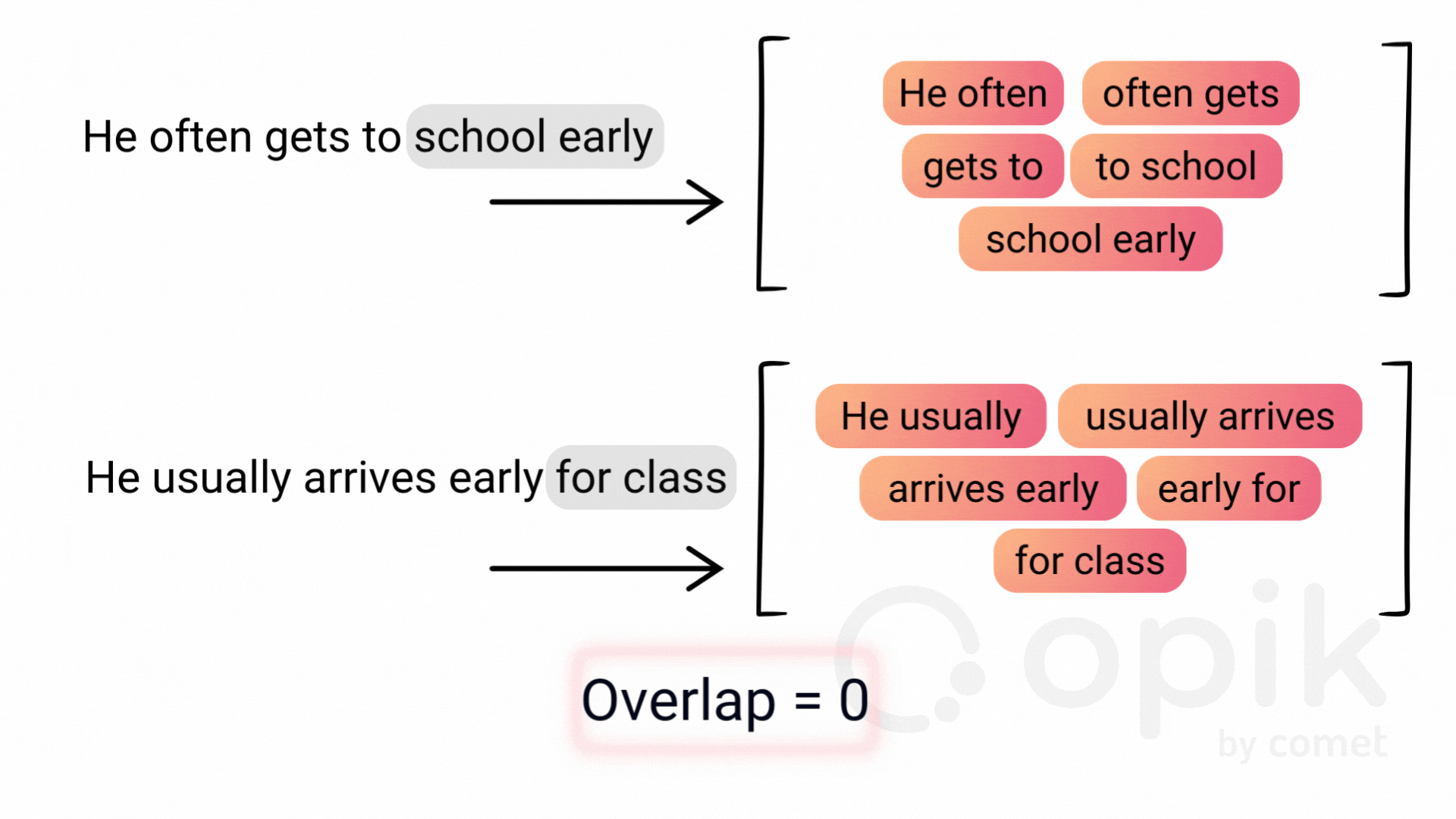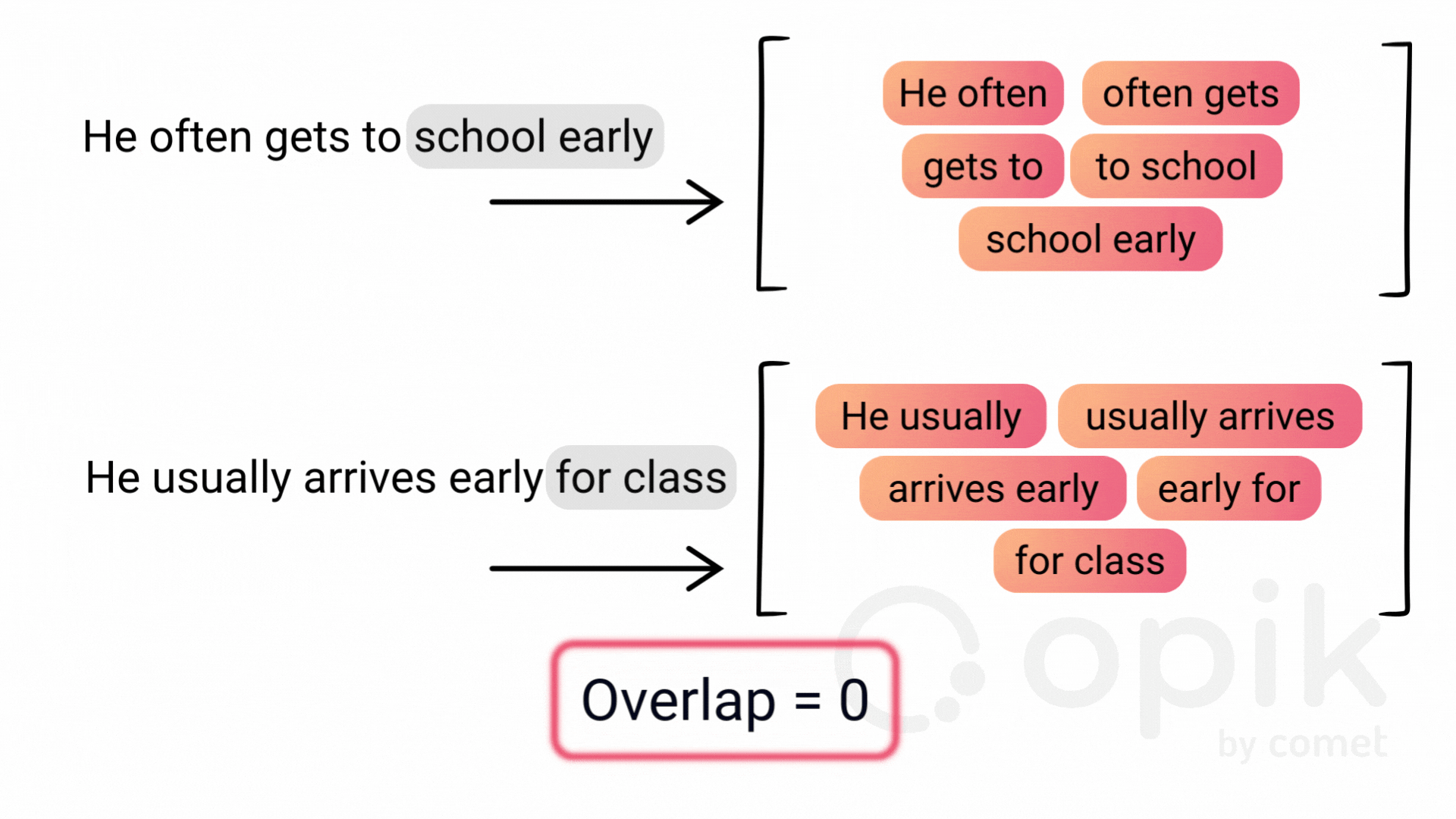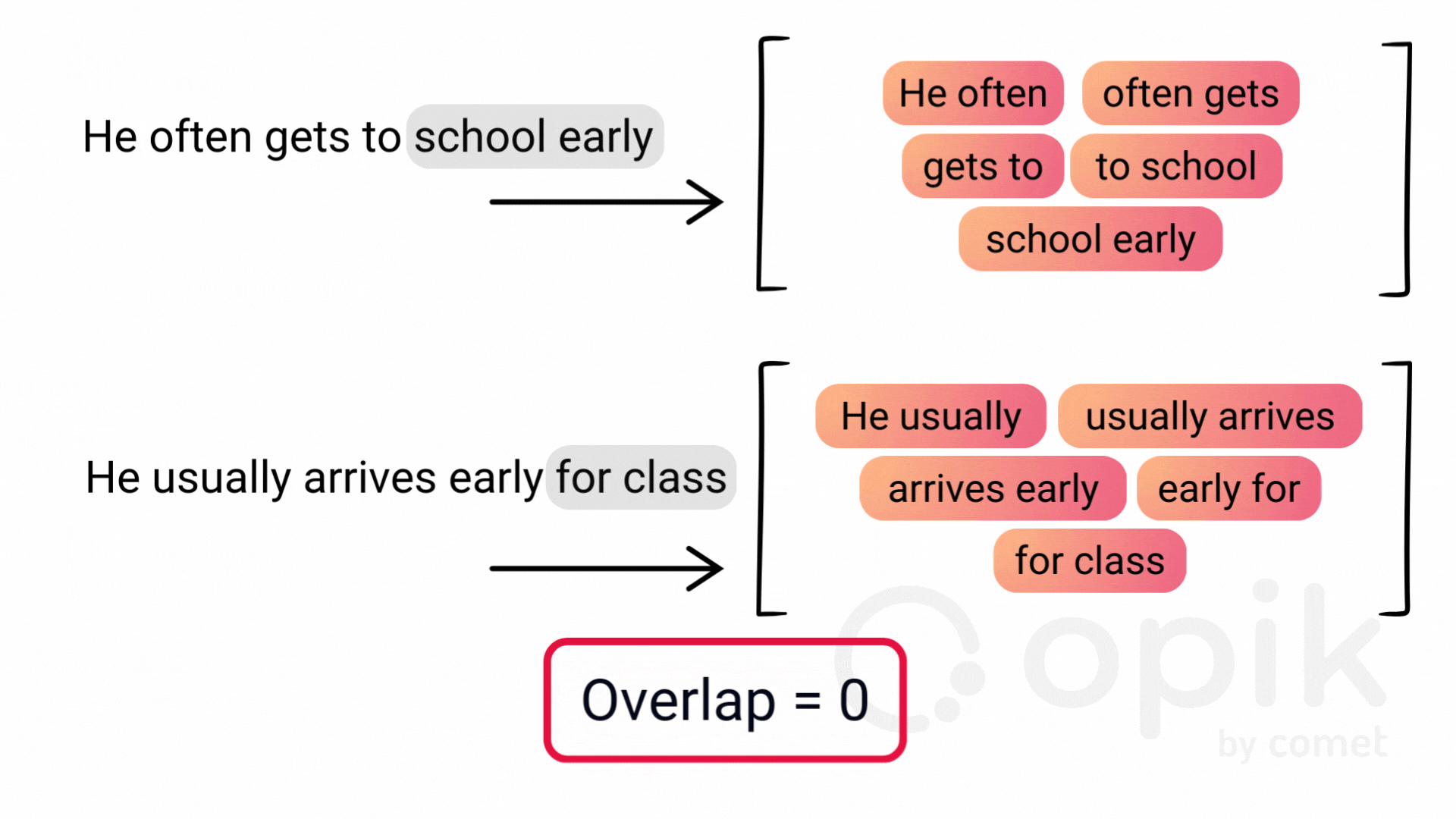
Prior to BERTScore, the most popular evaluation metrics for text generation were heuristic metrics like n-gram or overlap-based metrics.
The Problem With N-grams
N-grams count the number of continuous sequences of n tokens that occur in both the reference and candidate sentences. It’s highly intuitive, but poses some major challenges. Smaller n values often fail to capture context, such as word order, while larger n values quickly become overly restrictive.
More critically, n-grams cannot account for linguistic nuances like paraphrasing, dependencies, and polysemy. This means they score words with multiple meanings identically and fail to recognize synonyms or paraphrases with similar meaning. These limitations make n-grams inadequate for evaluating the depth and complexity of modern language models.
Contextual Embeddings
To address these issues, BERTScore leverages contextual embeddings. Unlike static embeddings, such as those from Word2Vec or GloVe, contextual embeddings are generated by transformer models, which use attention mechanisms to capture the relationships between all words in a sentence. This approach provides greater flexibility and nuance, making it more suitable for complex tasks like language understanding.
While a deeper exploration of embeddings is beyond the scope of this article, in simple terms, embeddings are vectors of floating-point numbers that capture the semantic context of individual tokens.
Cosine Similarity
After BERTScore has used a transformer-based model (originally a BERT model) to generate contextual embeddings, how does it use them to quantify sentence similarity?
As mentioned, contextual embeddings are high-dimensional vectors of floating-point numbers. To measure their similarity, we apply basic linear algebra by calculating the cosine of the angle between two vectors. Vectors that are closer in the embedding space have a higher semantic similarity. This measure is the cosine similarity.

Once the cosine similarity has been calculated between each token in the candidate sentence and each token in the reference sentence, greedy matching is used to select the highest cosine similarity score for each token.
The core benefit of BERTScore is that it gives you the richness of a learned metric via contextual embeddings, with the computational efficiency of a heuristic metric like cosine similarity.
The final steps include using the maximum similarity scores of each token to compute BERTRecall, BERTPrecision, and BERTF1, and optional importance weighting and baseline rescaling, which we’ll cover in the next section.
Implement BERTScore From Scratch in Python
Using what we’ve learned so far about BERTScore, let’s implement it from scratch in Python to help build intuition for what it’s actually doing under the hood. Later, we’ll implement BERTScore as a custom metric in Opik, and test it out on an image-captioning dataset.
First, we’ll need to choose our BERT-based model. Here we choose a medium-sized BERT model for English texts and load its accompanying tokenizer:
import torch
from transformers import BertTokenizer, BertModel
# Load BERT model and tokenizer
MODEL_NAME = "bert-base-uncased"
tokenizer = BertTokenizer.from_pretrained(MODEL_NAME)
model = BertModel.from_pretrained(MODEL_NAME, device_map="auto")
You can find a full list of supported models, along with their performance scores and best representation layers here.
BERT Embeddings and Cosine Similarity
Next, to calculate BERTScore, we’ll define several functions to help out with each step of the process. Leaving out the optional steps mentioned above, this includes:
- Getting embeddings of each sentence
- Calculating cosine similarity between embeddings
- Using greedy matching to select highest score
- Calculating BERTRecall, BERTPrecision, BERTF1 and return in a dictionary.
Let’s start with a function to compute the embeddings of each reference and candidate sentence. We’ll need to tokenize the text, create embeddings of the tokens, and return the first dimension of the model’s output, which corresponds to the last hidden state.
def get_embeddings(text):
"""
Generate token embeddings for the input text using BERT.
Args:
text (str): Input text or batch of sentences.
Returns:
torch.Tensor: Token embeddings with shape (batch_size, seq_len, hidden_dim).
"""
# Tokenize input text
inputs = tokenizer(text, return_tensors="pt", padding=True, truncation=True)
# Move inputs to GPU if available
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
inputs = inputs.to(device)
# Compute embeddings without gradient calculation
with torch.no_grad():
outputs = model(**inputs, output_hidden_states=True)
# Return last hidden states (token-level embeddings)
return outputs.last_hidden_stateNext, we’ll create a function to calculate the cosine similarity between generated embeddings. These embeddings will need to be reshaped and then normalized. Once normalized the cosine similarity between two vectors equals their dot product, so we can use basic matrix multiplication to create a matrix of cosine similarity scores.
def cosine_similarity(generated_embeddings, reference_embeddings):
"""
Compute cosine similarity between two sets of embeddings.
Args:
generated_embeddings (torch.Tensor): Embeddings of candidate tokens with shape (batch_size, seq_len, hidden_dim).
reference_embeddings (torch.Tensor): Embeddings of reference tokens with shape (batch_size, seq_len, hidden_dim).
Returns:
torch.Tensor: Cosine similarity matrix with shape (seq_len_generated, seq_len_reference).
"""
# Normalize embeddings along the hidden dimension
generated_embeddings = torch.nn.functional.normalize(generated_embeddings, dim=-1)
reference_embeddings = torch.nn.functional.normalize(reference_embeddings, dim=-1)
# Compute similarity using batched matrix multiplication
return torch.bmm(generated_embeddings, reference_embeddings.transpose(1, 2))
We now have matrices containing the cosine similarity scores of each token in the candidate sentence with each token in the reference sentence. But we need a way to aggregate these values for a sentence-level representation of similarity. The original authors of the BERTScore paper proposed three measures: BERTRecall, BERTPrecision, and BERTF1 to do just this.
BERTPrecision, BERTRecall, BERTF1
Traditionally, precision, recall, and F1 scores evaluate a classifier’s ability to distinguish between positive and negative samples. While BERTScore isn’t designed for classification, its authors adapted these metrics for evaluating LLM-generated text, preserving their original intent in this new context.

Let’s start with precision. Precision measures a model’s accuracy in identifying true positives. In BERTScore, “true positives” are candidate tokens that align with reference tokens. BERTprecision quantifies how much of the candidate’s content is semantically meaningful relative to the reference. It is calculated as the average of the maximum cosine similarities between each candidate token’s embedding and the embeddings of all reference tokens. A high BERTPrecision indicates that the candidate is concise and relevant.

def get_precision(similarity_matrix):
"""
Calculate BERT precision as the mean of the maximum similarity scores from the candidate to the reference.
Args:
similarity_matrix (torch.Tensor): Cosine similarity matrix.
Returns:
torch.Tensor: Precision score.
"""
return similarity_matrix.max(dim=2)[0].mean()
Next, let’s define BERTRecall. Recall measures the proportion of actual positive instances that a model identifies correctly. For BERTScore, BERTRecall reflects how much of the reference’s meaning is captured by the candidate. It is calculated as the average of the maximum cosine similarity scores between each reference token’s embedding and the embeddings of all candidate tokens. A high BERTRecall suggests that the candidate does not miss key information present in the reference.

def get_recall(similarity_matrix):
"""
Calculate BERT recall as the mean of the maximum similarity scores from the reference to the candidate.
Args:
similarity_matrix (torch.Tensor): Cosine similarity matrix.
Returns:
torch.Tensor: Recall score.
"""
return similarity_matrix.max(dim=1)[0].mean()
The BERTF1 score is the harmonic mean of BERTPrecision and BERTRecall, balancing these two metrics when there is a trade-off. It provides a single summary value of overall semantic alignment between the candidate and the reference.

def get_f1_score(precision, recall):
"""
Compute the F1 score given precision and recall.
Args:
precision (torch.Tensor): Precision score.
recall (torch.Tensor): Recall score.
Returns:
torch.Tensor: F1 score.
"""
return 2 * (precision * recall) / (precision + recall)
Finally, BERTScore outputs BERTPrecision, BERTRecall, and BERTF1 as a dictionary, which we’ll cover in the next coding section.
Importance Weighting and Baseline Rescaling with BERTScore
Additionally, BERTScore includes some optional processes including importance weighting with IDF and baseline rescaling.
Since rare words are often more indicative of sentence meaning than common words or stop words, BERTScore allows for frequency penalization using Inverse Document Frequency (IDF) of the test corpus (body of reference sentences).
IDF is based on the principle that words appearing in many documents are less informative than words that appear in fewer documents. It’s calculated by taking the logarithm of the total number of documents, N, divided by the number of documents containing a given term, t.

Additionally, to normalize the scores to a range of -1 to 1 and make them more readable, the original BERTScore paper suggests rescaling BERTScore with respect to its empirical lower bound b as a baseline. This calculation does not affect score ranking however, and is solely meant to improve readability. A full list of baseline scores for BERT models in 12 languages can be found in this directory.


Both of these processes are set to False by default in Hugging Face’s implementation of BERTScore, so we won’t include them when we code BERTScore from scratch. Each can be set to True with the idf and rescale_with_baseline parameters of evaluate.bertscore, respectively.
Putting It All Together
Now that we have all of our helper functions, let’s put them together to create our BERTScore function. In this function we will:
- Generate embeddings of the candidate and reference tokens using the model we instantiated above.
- Calculate the cosine similarity matrix (or, after normalization, the dot product) between each candidate embedding and each reference embedding.
- Using greedy matching, calculate the precision, recall, and f1 scores of each sentence
- Return the dictionary of values.
def bert_score(candidate, reference):
"""
Compute BERTScore (Precision, Recall, F1) between a candidate and a reference sentence.
Args:
candidate (str): Candidate sentence.
reference (str): Reference sentence.
Returns:
dict: Dictionary containing precision, recall, and F1 scores.
"""
# Get token embeddings for candidate and reference
candidate_embeddings = get_embeddings(candidate)
reference_embeddings = get_embeddings(reference)
# Compute cosine similarity matrix
similarity_matrix = cosine_similarity(candidate_embeddings, reference_embeddings)
# Calculate precision, recall, and F1 scores
precision = get_precision(similarity_matrix)
recall = get_recall(similarity_matrix)
f1_score = get_f1_score(precision, recall)
# Return scores as a dictionary
return {
"precision": precision.item(),
"recall": recall.item(),
"f1_score": f1_score.item(),
}
# Example usage
if __name__ == "__main__":
candidate_sentence = "The cat sat on the mat."
reference_sentence = "A cat rested on a mat."
scores = bert_score(candidate_sentence, reference_sentence)
print("BERTScore:", scores)
Feel free to test this function out for yourself! Note that the intention of this exercise is to help build intuition around what BERTScore does under the hood, and it is significantly simplified from the HuggingFace.evaluate version, which incorporates IDF, baseline rescaling, batching, padding, attention mask shifting, and more.
For these reasons, we will be using the Hugging Face implementation of BERTScore to build a custom metric in Opik below.
Implement BERTScore in Opik
Now let’s try a real-life end-to-end example. If you aren’t already, you can follow along with the Colab here.
In this section, we’ll use BLIP, an image-captioning model, along with a small subset of the Conceptual Captions dataset from Google Research, which pairs images with captions sourced from the internet. Notably, image captioning and machine translation were the original use cases proposed by BERTScore’s authors.
To do this, we’ll implement BERTScore in Opik, Comet’s open-source LLM evaluation framework. We’ll leverage Hugging Face’s evaluate implementation of BERTScore, modifying it slightly to create a custom Opik metric with a score method that returns a ScoreResult object:
from evaluate import load
bertscore = load("bertscore")
from opik.evaluation.metrics import base_metric, score_result
from typing import List, Union
class BERTScore(base_metric.BaseMetric):
"""
BERTScore is a semantic similarity evaluation metric for text generation tasks.
It measures the similarity between predicted (candidate) and reference texts
by comparing their contextual embeddings using a pre-trained language model.
This implementation leverages the Hugging Face Evaluate library for computing BERTScore.
For more details:
- Original BERTScore paper: https://arxiv.org/abs/1904.09675
- Hugging Face implementation: https://github.com/huggingface/evaluate/blob/main/metrics/bertscore/README.md
Args:
name (str): The name of the metric, defaults to "BERTScore".
language (str): The language of the model, defaults to "en" (English).
"""
def __init__(
self,
name: str = "BERTScore",
language: str = "en"
):
self.name=name
self.language = language
def score(
self, candidate: str, reference: str, **kwargs
) -> List[score_result.ScoreResult]:
"""
Computes the BERTScore between a candidate (predicted) text and a reference (ground truth) text.
This method calculates recall, precision, and F1 score based on token-level
contextual embeddings, using a pre-trained transformer model.
Args:
candidate (str or List[str]): The candidate text or list of texts to evaluate.
Must not be empty or contain only whitespace.
reference (str or List[str]): The reference text or list of texts to compare against.
Must not be empty or contain only whitespace.
**kwargs: Additional keyword arguments for the Hugging Face BERTScore computation.
Returns:
List[score_result.ScoreResult]: A list of `ScoreResult` objects containing:
- BERTRecall: The BERTScore recall score.
- BERTPrecision: The BERTScore precision score.
- BERTF1: The BERTScore F1 score.
Raises:
ValueError: If candidate or reference inputs are empty strings or lists.
TypeError: If candidate or reference inputs are not strings or lists of strings.
"""
# Validate and normalize inputs
def validate_and_normalize(text: Union[str, List[str]]) -> List[str]:
if isinstance(text, str):
if not text.strip():
raise ValueError("Input text cannot be empty or whitespace.")
return [text]
if isinstance(text, list):
if not all(isinstance(t, str) and t.strip() for t in text):
raise ValueError("All elements in the input list must be non-empty strings.")
return text
raise TypeError("Input must be a string or a list of strings.")
candidate = validate_and_normalize(candidate)
reference = validate_and_normalize(reference)
results_dict = bertscore.compute(predictions=candidate, references=reference, lang=self.language)
# Create score results
return [
score_result.ScoreResult(value=results_dict["recall"][0], name="BERTRecall"),
score_result.ScoreResult(value=results_dict["precision"][0], name="BERTPrecision"),
score_result.ScoreResult(value=results_dict["f1"][0], name="BERTF1"),
]
bscore = BERTScore()
After defining BERTScore as a custom metric, we can use it by:
- Defining the model’s forward pass in your_llm_application (after some minor image pre-processing).
- Calling our application in evaluation_task and returning a dictionary with keys that match the parameters expected by our custom BERTScore metric above.
- Add tracking by decorating our functions with Opik’s @track decorator to automatically log relevant data to the platform.
- Pass the evaluation_task function to Opik’s evaluate function, which runs and logs the full evaluation process, including calculating perplexity scores for each call.
- Note that we also pass our model’s configuration details to the evaluate function to log them to Opik.
You can find the full code in the Colab.
from opik import track
import requests
from PIL import Image
from opik.evaluation import evaluate
# Configuration constants for text generation
MAX_LENGTH = 50
MIN_LENGTH = 10
LENGTH_PENALTY = 1.0
REPETITION_PENALTY = 1.2
NUM_BEAMS = 5
EARLY_STOPPING = True
# Model name
MODEL_NAME = "your_model_name_here" # Replace with your actual model name
@track
def generate_caption(image_url: str) -> dict:
"""
Generates a caption for an image using a pre-trained LLM.
Args:
image_url (str): The URL of the image to caption.
Returns:
dict: A dictionary containing the generated caption as 'candidate'.
"""
# Load image from the provided URL
try:
response = requests.get(image_url, stream=True)
response.raise_for_status()
image = Image.open(response.raw)
except requests.exceptions.RequestException as e:
raise ValueError(f"Error fetching image from URL: {e}")
# Preprocess the image
inputs = processor(images=image, return_tensors="pt").to("cuda")
# Generate text using the model
outputs = model.generate(
**inputs,
max_length=MAX_LENGTH, # Maximum length of generated text
min_length=MIN_LENGTH, # Minimum length of generated text
length_penalty=LENGTH_PENALTY, # Length penalty to control verbosity
repetition_penalty=REPETITION_PENALTY, # Penalty to avoid repetition
num_beams=NUM_BEAMS, # Number of beams for beam search
early_stopping=EARLY_STOPPING # Stop generation early when appropriate
)
# Decode and return the caption
caption = processor.decode(outputs[0], skip_special_tokens=True)
return {"candidate": caption}
@track
def evaluation_task(data: dict) -> dict:
"""
Evaluation task to compare generated captions with reference captions.
Args:
data (dict): A dictionary containing 'image_url' and 'reference' keys.
Returns:
dict: A dictionary with 'reference' and 'candidate' captions.
"""
# Generate LLM output (caption)
llm_output = generate_caption(data['image_url'])
# Return the reference and candidate captions
return {
"reference": data['reference'],
"candidate": llm_output['candidate']
}
# Run evaluation
evaluation = evaluate(
experiment_name="My BERTScore Experiment", # Name of the experiment
dataset=dataset, # Dataset for evaluation
task=evaluation_task, # Evaluation task
scoring_metrics=[bscore], # Scoring metrics to use
experiment_config={ # Configuration for the experiment
"model": MODEL_NAME,
"max_length": MAX_LENGTH,
"min_length": MIN_LENGTH,
"length_penalty": LENGTH_PENALTY,
"repetition_penalty": REPETITION_PENALTY,
"num_beams": NUM_BEAMS,
"early_stopping": EARLY_STOPPING
},
task_threads=1, # Number of threads for the task
)
And here is what the output of your evaluation should look like from within the Opik UI:


BERTScore: Towards LLM-as-a-judge Metrics
BERTScore was among the first widely adopted evaluation metrics to incorporate large language models for assessing output quality. It operates by using a pre-trained transformer-based model, such as BERT, to generate contextual embeddings, or, dense, learned representations of tokens that encode semantic and syntactic information.
While innovative for its time, BERTScore represents an earlier stage in the progression of modern LLM evaluation methods. Unlike modern “LLM-as-a-judge” approaches, which rely on language models to generate comprehensive, nuanced feedback for another model’s outputs, BERTScore focuses solely on token-level comparisons without producing holistic judgments. This distinction underscores a shift toward evaluation techniques that prioritize coherence, reasoning, and context on a broader scale.
However, LLM-as-a-judge methods, while powerful, remain opaque, non-deterministic, and computationally expensive, making them less accessible and harder to interpret. In contrast, metrics like BERTScore remain essential for their efficiency, transparency, and utility in providing actionable insights into model behavior.
If you found this article useful, follow me on LinkedIn and Twitter for more content!


